2 Forelesning 23/1-23(2 timer). Transistorer, porter og krets som adderer tall

Avsnitt fra Tanenbaum: 1.3.1

2.1 Sist

• Operativsystemkjernen
• Prosesser
• Logiske porter

Slides brukt i forelesningen

2.2 Forelesningsvideoer

Uredigert opptak av hele forelesningen ( 01:34:15)

Opptak av forelesningen inndelt etter tema:

os2del1.mp4 (04:12) Innledning om kurssider, digitale forelesninger, oppgaver
os2del2.mp4 (03:55) Mål for forelesningen: adderings-krets
os2del3.mp4 (08:12) Slides: Transistoren, Moores lov og Integrerte kretser
os2del4.mp4 (03:37) Slides: CMOS, NMOS og PMOS
os2del5.mp4 (05:06) Slides: Hvordan bygge NOT-port or OR-port av CMOS-transistorer
os2del6.mp4 (01:13) Slides: Binær funksjon
os2del7.mp4 (02:15) Slides: Kort repetisjon av logikken for AND, OR og NOT
os2del8.mp4 (06:47) Slides: Sannhetstabell, logisk uttrykk og logisk sum
os2del9.mp4 (02:17) Slides: Tegne krets av logisk uttrykk
os2del10.mp4 (02:21) Slides: Tegne og forenkle kretser
os2del11.mp4 (02:56) Spørsmål fra pausen: Hvorfor blir Y = 1 når X = 0 i NOT-porten?
os2del12.mp4 (04:59) Gjennomgang av 2 poll-spørsmål (litt lite bilde i opptaket) (Eksamensoppgave 2 og 3 fra Eksamen våren 2020)
os2del13.mp4 (00:50) Spørsmål: Er de to kretsene like? Begge = B
os2del14.mp4 (02:01) Slides: Forenkle kretser med Boolsk algebra
os2del15.mp4 (02:39) Binær addisjon
os2del16.mp4 (01:36) Addisjonskrets
os2del17.mp4 (02:40) Generell metode for å lage krets: Sannhetstabell-boolsk uttrykk-forenkling-tegne krets
os2del18.mp4 (03:28) Bruk av Full Adder for å legge sammen tall
os2del19.mp4 (02:46) Adderings-krets og andre nødvendige kretser
os2del20.mp4 (08:06) Demo: Hvordan lage og bruke kretser i Digital Works

2.3 Porter og transistorer

Ved hjelp av AND, OR og NOT-porter kan uttrykke alle mulige logiske sammenhenger. Fysisk sett er disse logiske portene bygd fra enda mindre byggestener, transistorer. Dette er selve grunn-byggestenen i en datamaskin på lignende måte som atomer er grunn-byggestenen i alle materialer. En transistor er egentlig bare en av/på bryter hvor en innkommende ledning er en bryter som avgjør om det ledes strøm eller ikke. Dette er omtrent som en vanlig elektrisk bryter på veggen, men i transistorens tilfelle styres bryteren av om det kommer strøm inn eller ikke. Slike transistorer kan man sette sammen i kretser og bygge logiske porter som igjen kan brukes til all den logikk en CPU trenger.

I de aller første datamaskiner ble radiorør brukt som slike brytere. I 1948 ble halvleder-transistoren oppfunnet av Bardeen, Brattain og Shockley, noe de fikk nobelprisen i fysikk for i 1956. Man kan argumentere for at dette er den viktigste enkeltstående oppfinnelsen noen sinne. Den største forskjellen fra radiorør er at transistorene kan lages ekstremt små; i 2017 klarte Intel og pakke mer enn 100 millioner transistorer på en kvadratmillimeter. Dette var med såkalt 10 nanometer teknologi hvor størrelsen på komponenter er helt nede i 10 nanometer (en nanometer er $10^{-9}$ meter). I 2020 begynte TSMC (Taiwan Semiconductor Manufacturing Company) produksjon av 5 nanometer silisium-brikker (chips). TSMC er verdens ledende halvleder-produsent og produserer for kunder som AMD og Apple og produserer også noe for Intel og andre firma som i hovedsak har egen produksjon.

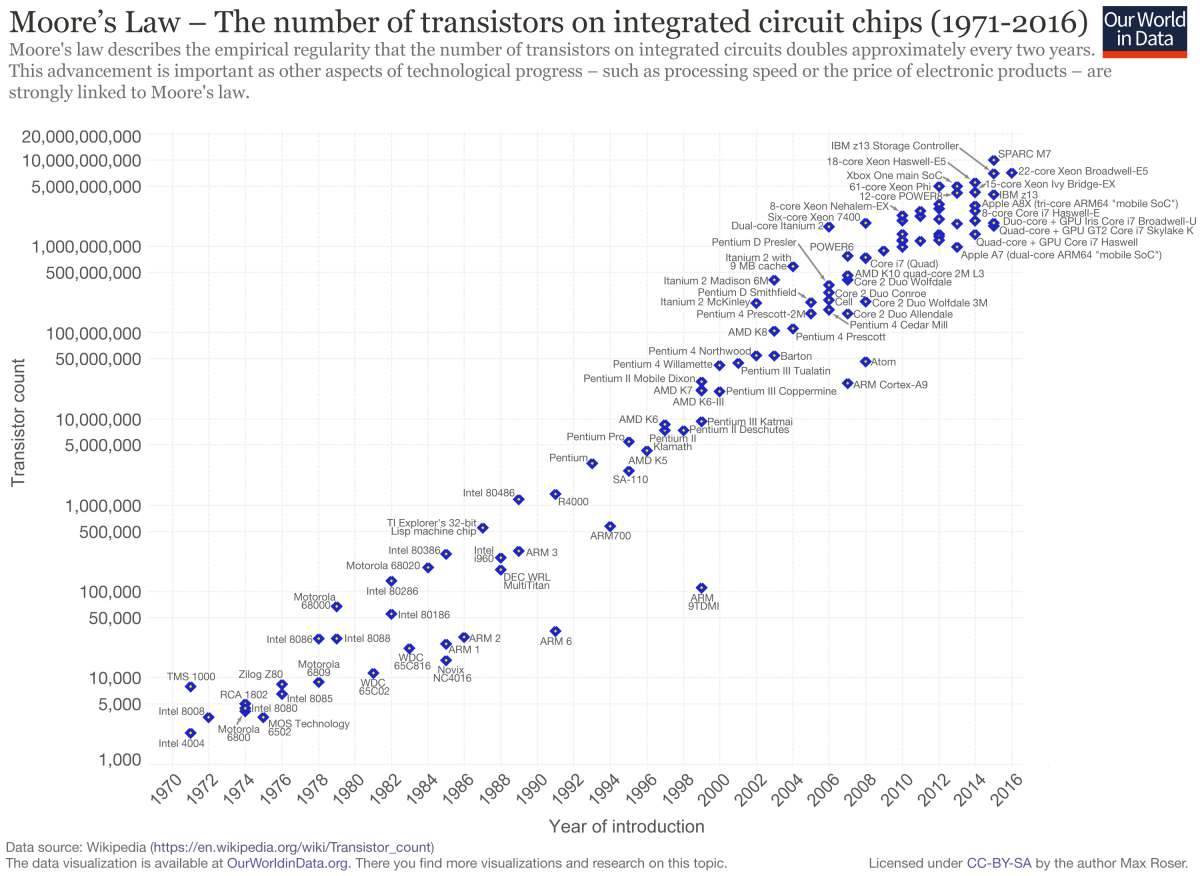
I CPU-en Intel 4004 fra 1971 var det 2.300 transistorer og en CPU klokkefrekvens på 500 KHz, mens det i en Intel Xeon fra 2016 var 7.2 milliarder transistorer og en klokkefrekvens på 3 GHz. Mindre avstander gjør det mulig å øke klokkefrekvensen, men etter 2005 har den ikke øktet fordi det genreres for mye varme. I følge Moores lov så dobler antall transistorer i integrerte kretser seg hvert andre år og den loven har blitt fulgt ganske nøyaktig siden 70-tallet. Riktignok har det meste av ekstra transistorer i moderne CPUer blitt brukt til cache, hurtigminne i CPUene. Fig. 8 ¹ viser eksempler på mikroprosessorer som følger Moores lov.

Figure: Moores lov: antall transistorer i integrerte kretser dobler seg hvert andre år. T

Og snart når man de fysiske yttergrensene. Bohr-radius, avstand fra kjerne til elektron i hydrogen, er 0.05 nanometer. Radius til et Silisium-atom er 0.11 nanometer. Komponentene har nå blitt så små at man må ta hensyn til fenomener som kvante-tunnelering og man kan ikke gå særlig mye lenger ned i størrelse på transistor-teknologien.

2.4 CMOS

CMOS er en teknologi for å lage integrerte kretser som brukes i alle mikroprosessorer. At den er komplementær betyr at den setter sammen to motsatte typer transistorer, NMOS og PMOS. En NMOS-transistor er egentlig en n-type metal oxide semiconductor field effect transistor (MOSFET). Dette er egentlig en ekstremt liten bryter, noen tiltalls nanometer stor. Hvis det er null spenning inn på transistoren, er de to andre utgangene isolert fra hverandre, bryteren er av. Hvis man sender positiv spenning inn skrus bryteren på og de to andre utgangene vil lede strøm, akkurat som når man trykker på en lysbryter. En n-type transistor er vist i Fig. 9.

Figure: NMOS transistor. Når det ikke er spenning inn, er øvre og nedre del isolert, bryteren er av. Når X kobles til spenning går bryteren på og strøm ledes mellom nedre og øvre del.

Det at man kan lage så ekstremt små transistorer har gjort det mulig å legge milliarder av dem på samme chip og lage enormt kraftige mikroprosessorer. En p-type transistor er veldig lik, men den virker helt motsatt, den er komplementær. En slik transistor er vist i Fig. 10.

Figure: PMOS transistor. Virker motsatt av NMOS, når det er spenning inn, er øvre og nedre del isolert, bryteren er av.

Ved å sette sammen NMOS og PMOS sammen viste det seg at man unngår unødvendig strømføring i kretsene og at man dermed reduserer varmeproduksjonen som er et vesentlig problem for integrerte kretser. Man kan lage den enkleste logiske porten, NOT, ved å sette sammen en p-type og en n-type transistor som vist i Fig. 11.

Figure: NOT-port. Når X kobles til positiv spenning, vil den øverste PMOS-transistoren isolere, mens den nederste NMOS-transistoren gir 0 spenning ved Y. Og det motsatte skjer når X kobles til jord.

Dermed har man en viktig byggestein. I figuren ser man også hvordan de forskjellig delene kobles sammen i en krets og kobles til spenning eller jord, null spenning. Hvis man kobler X-inngangen til NOT-porten til jord, null volt, vil man måle 5 volt ved utgangen Y. Så kan man bygge videre, ved for eksempel å sette en NOT-port til etter den første. Men hvis man ønsker å kunne lage alle mulige logiske binære funksjoner, trenger man også AND- og OR-porter. Det viser seg at man kan lage AND og OR-porter med 3 CMOS-par av transistorer og hvordan man kan lage OR er vist i Fig. 12. Omtrent tilsvarende kan man lage en AND-port.

Figure: En OR-port kan lages av 6 transistorer. Vss er jord, null spenning, og Vdd er positiv spenning.

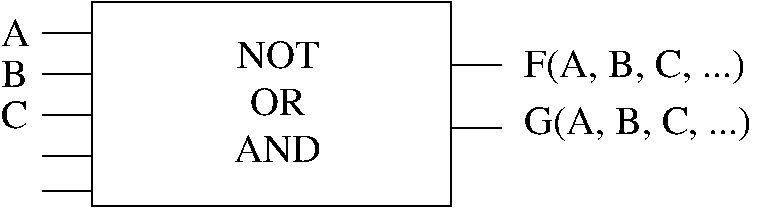
Dermed kan man lage alle mulige logiske operasjoner bygget på transistorer ved å sette sammen systemer av NOT, AND og OR-porter. For å bygge en CPU som kan gjøre operasjoner som å legge sammen tall, trenger man generelt å lage generelle binære funksjoner som vist i Fig. 14.

Figure: En generell binær funksjon.

Generelt kan en boolsk funksjon defineres ved en sannhetstabell som definerer hva output av funksjonen skal være for alle mulige kombinasjoner av binær input.

2.5 Boolsk algebra

I boolsk algebra uttrykkes AND, OR og NOT på følgende måte

• AND: A $\cdot$ B (A $\land$ B )
• OR: A + B (A $\lor$ B)
• NOT: $\overline{\mbox{A}}$ ($\lnot$ A )

De boolske operatorene som står i parentes er slik de blir brukt i kurset Diskret matematikk. I digitalteknikk er det vanligst å bruke konvensjonen for boolske operatorer som brukes i dette kurset.

2.6 Fra sannhetstabell til logisk krets.

Når man skal lage en komponent av en CPU, må man spesifisere nøyaktig hvordan denne kretsen skal virke. Og generelt vet man nøyaktig hva man ønsker. Hvis en krets for eksempel skal sammenligne to bit for å se om de er like, vil disse to bit være input til kretsen. Output vil være 1 (sann) hvis de to innkommende bit er like og 0 (usann) ellers. Tilsvarende kan man for mer komplekse kretser alltid kunne skrive ned hva som skal være output for hver eneste mulige input. På samme måte som for AND, OR og NOT-porter, kan ønsket om hvordan kretsen skal fungere formuleres som en såkalt sannhetstabell. Funksjonen F(A,B) til en krets som har som input A og B og som skal være 1 (sann) når A og B er like og 0 (usann) når A og B er forskjellige kan skrives slik:

A	B	F(A,B)
0	0	1
0	1	0
1	0	0
1	1	1

Ut ifra en slik sannhetstabell kan man alltid skrive ned et logisk uttrykk for funksjonen F(A,B). For å få til det, benytter man seg av egenskapene til AND og OR operatorene. Et produkt $A\cdot B$ vil kun være lik 1 hvis både A og B er lik 1, i alle andre tilfeller vil produket være lik 0. Hvis en linje i sannhetstabellen viser at F skal være lik 1, kan man derfor skrive ned et produkt som gir 1 når man ganger sammen (AND'er) nøyaktig de to verdiene i denne linjen av sannhetstabellen. For første linje i sannhetstabellen over, må man derfor skrive ned uttrykket

  $$\overline{A}\cdot \overline{B}$$ (1)

som første ledd av uttrykket F(A,B), siden dette gir 1 for verdiene A = 0 og B = 0 i første linje og 0 i alle andre tilfeller ( $\overline{A}$ betyr ikke A eller NOT A og er lik 1 når A = 0). Hvis man skriver ned tilsvarende uttrykk for alle linjer som gir 1 i sannhetstabellen, kan man til slutt legge sammen alle leddene med OR-operatoren. Dette blir da tilsammen et korrekt uttrykk for funksjonen F, fordi om minst ett av leddene i et OR-uttrykk er 1 vil det totale uttrykket også bli 1. Dermed vil en slik sum av produkter alltid gi den riktige verdien for funksjonen F. I sannhetstabellen for sammenligningskretsen, gir også den siste linjen 1. Denne linjen gir derfor uttrykket $A\cdot B$ som er 1 når A og B er 1 og ellers 0. Dermed kan det logiske uttrykket for funksjonen skrives ned som

  $$F(A,B) = \overline{A}\cdot \overline{B} + A \cdot B$$ (2)

For å overbevise seg om at dette er riktig, kan man ganske enkelt teste at hvert ledd i sannhetstabellen er oppfylt. En stor fordel med logiske operatorer er at antall mulig input-verdier er begrenset, i motsetning til for kontinuerlige funksjoner.

Når man har klart å skrive ned et logisk uttrykk for sannhetstabellen, kan man ganske enkelt tegne et diagram for kretsen ved å erstatte operatorene AND, OR og NOT med de tilsvarende logiske portene. Dermed kan man tegne følgende krets for ligning Eq. 2:

Figure: Tegning av den logiske kretsen $F(A,B) = A \cdot B + \overline {A}\cdot \overline {B}$.

Slike kretsdiagram kan brukes til å spesifisere enkeltdelene i en større krets som en CPU og til slutt kan tilsvarende deler lages i hardware. Først legges de logiske delene som skal med og så kobles de sammen; 'place and route' kalles generelt denne teknikken. Det finnes også programmeringsspråk som brukes til å definere kretser og verktøy som automatiserer deler av prosessen fra en logisk krets til en fysisk implementasjon som en integrert krets.

2.7 Forenkling av logiske uttrykk.

Man kan generelt skrive ned logiske uttrykk som beskrevet over fra en sannhetstabell, også om den har 3, 4 eller enda flere input. Men da blir de resulterende logiske kretsene generelt svært omfattende. Men ved hjelp av Boolsk algebra og andre metoder er det mulig å redusere størrelsen før kretsene lages. Konstruksjonen av følgende krets er et eksempel på dette. Anta at man ønsker å lage en krets som tilfredsstiller følgende sannhetstabell:

A	B	F(A,B)
0	0	0
0	1	1
1	0	0
1	1	1

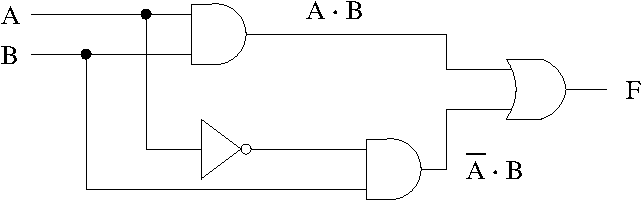
Ved å følge metoden forklart i forrige avsnitt, kan man da skrive ned den logiske funksjonen for kretsen som en sum av de to leddene som gir verdien 1 for andre og fjerde linje, slik at sannhetstabellen oppfylles:

  $$F(A,B) = \overline{A}\cdot B + A \cdot B$$ (3)

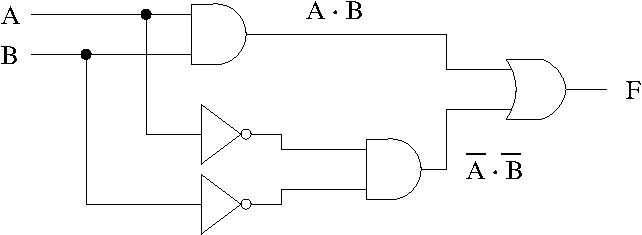
Dermed kan man tegne følgende krets for ligning Eq. 3:

Figure: Tegning av den logiske kretsen $F(A,B) = A \cdot B + \overline {A}\cdot B$.

I motsetning til uttrykket i forrige avsnitt, kan dette uttrykket forenkles, slik at hele kretsen kan forenkles. Som i vanlig algebra, finnes det metoder for å faktorisere og forenkle uttrykk. Ved å bruke slike metoder kan dette uttrykket forenkles som følger:

  $$F(A,B) = \overline{A}\cdot B + A \cdot B = ( \overline{A} + A) \cdot B = 1 \cdot B = B$$ (4)

Her har vi brukt at at $\overline{A} + A = 1$ som gjelder kun for Boolsk algebre. Som i vanlig algebra kan man faktorisere og som i vanlig algebra gjelder $1 \cdot X = X$. I dette tilfellet er altså funksjonen F = B og kretsen blir ekstremt forenklet som vist i Fig. 16.

Figure: Ekstrem forenkling av kretsen til $F(A,B) = B$.

Man kan på samme måte lage boolske funksjoner og tegne kretser med utgangspunkt i en sannhetstabell når man har 3, 4 og også flere variabler. Med 3 og 4 variabler kan man bruke såkalte Karnaugh-diagram for systematisk forenkling, noe som er raskere og enklere enn å bruke Boolsk algebra direkte på utrykkene. Ofte er 4 variabler nok til å lage den enheten man ønsker og siden kan man bruke 'place and route' for å koble sammen alle enhetene til en fullstendig krets, slik som en CPU.

2.8 Hvordan kan man få en logisk krets til å addere?

I digital logikk er tall representert binært, som spenninger av og på. En måte å få en krets til å legge sammen binære tall på, er å la den gjennomføre operasjonene som man bruker når man legger sammen binære tall med penn og papir. Fig. 17 viser hvordan man legger sammen 1 + 3 = 4 binært. Det rød ett-tallet over nullen er mente fra første operasjon der man gjør 1 + 1 = 10 binært og får en i mente. Tilsvarende er det andre røde tallet mente fra neste operasjon.

Figure: Binær addisjon som gir 1 + 3 = 4

Nå vil det være mulig å lage en digital krets som utfører en enkelt av disse repeterende operasjonene som man gjør for å legge sammen to tall. Man tar med mente fra høyre, legger sammen med de to tallen som står under hverandre og det resulterer i ett binært siffer som settes under brøkstreken og eventuelt mente til neste operasjon. Det betyr at input for kretsen er mente fra forrige operasjon (som vi kaller Z) og de to tallene som skal adderes, dem kaller vi X og Y. Output fra kretsen er ett tall S som skal under brøkstreken og resulterende mente som vi kaller C (engelsk: carry). Operasjonen som skal utføres er vist i Fig 18.

Figure: En enkelt operasjon i binær addisjon som må repeteres for hvert siffer i de binære tallene.

Når man forstår algoritmen for å legge sammen to tall, er det rett frem å skrive ned sannhetstabellen for en krets som skal gjøre akkurat denne operasjonen, med input X, Y og Z og output S og C. Den blir som følger:

X	Y	Z	S	C
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

For eksempel i den siste linjen, når alle tre input er 1, forplanter mente seg videre til C = 1 og også S blir 1. Gitt en slik sannhetstabell kan man med metodene vist i de forrige avsnittene konstruere en logisk krets ved å

1. Skrive ned boolske uttrykk for funksjonene S(X,Y,Z) og C(X,Y,Z).
2. Forenkle uttrykkene med Boolsk algebra (eller Karnaugh-diagram).
3. Tegne en krets basert på det Boolske uttrykket som utfører nøyaktig denne operasjonen.

Punkt 1 vil være å ta utgangspunkt i de fire linjene i sannhetstabellen som gir 1 for funksjonene S og C. Dermed kan man skrive ned uttrykkene:

$$\begin{eqnarray*} S(X,Y,Z) &=& \overline{X} \cdot \overline{Y}\cdot Z + \overlin... ...ine{Y} \cdot Z + X \cdot Y \cdot \overline{Z} + X\cdot Y\cdot Z \end{eqnarray*}$$

deretter kan uttrykkene forenkles. Det er ved hjelp av boolsk algebra (eller Karnaugh-diagram) mulig å forenkle C til

$$C(X,Y,Z) = X\cdot Y + Z\cdot Y + X\cdot Z$$

og dermed tegne kretsen som gir funksjonen C, som vist i Fig. 19. Det er uten for dette kursets pensum å utføre denne type litt mer kompliserte forenklinger, men det er viktig å vite at man systematisk kan utføre denne type forenklinger ved hjelp av boolsk algebra eller enda mer effektivt ved hjelp av Karnaugh-diagram.

Figure: Krets som lager funksjonen $C(X,Y,Z) = X\cdot Y + Z\cdot Y + X\cdot Z$.

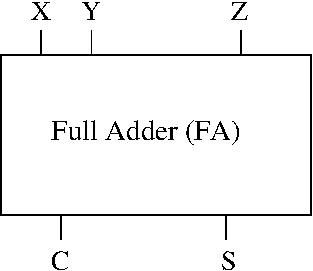
Uttrykket for S kan også forenkles noe. Deretter kan man tegne kretsene for disse uttrykkene sammen i en boks. I dette tilfellet kalles kretsen en Full Adder (FA) og en boks om gjør denne operasjonen (og hvor innholdet i kretsen med alle AND, OR og NOT-porter er skjult), kan se ut som i Fig. 20.

Figure: En Full Adder krets som oppfyller sannhetstabellen vist over.

Ved å sette sammen to slike Full Adder kretser ved å koble carry fra den høyre boksen til mente i den venstre boksen, som vist i Fig. 21, vil vi få en krets som legger sammen to binære tall $X_1 X_0$ og $Y_1 Y_0$ og som gir som resultat det binære tallet $S_2 S_1 S_0$.

Figure: To Full Adder kretser skjøtet sammen slik at de regner ut det binære regnestykket $X_1 X_0 + Y_1 Y_0 = S_2 S_1 S_0$ korrekt for alle mulige verdier av X og Y.

Kretsen med de to FA'ene utfører regnestykket som er vist i Fig. 22

Figure: Det binære regnestykket $X_1 X_0 + Y_1 Y_0 = S_2 S_1 S_0$. Kretsen i Fig. 21 utfører dette.

For å addere tall med flere bit, kan man bare legge til flere slike bokser, en for hvert tall. Om man skjøter sammen 64 slike Full Adder bokser, får man en krets som legger sammen 64-bits tall. I Fig. 23 legger kretsen sammen to 3-bits tall.

Figure: Tre Full Adder kretser skjøtet sammen slik at de regner ut det binære regnestykket $X_2 X_1 X_0 + Y_2 Y_1 Y_0 = S_3 S_2 S_1 S_0$ korrekt for alle mulige verdier av X og Y.

Her har vi sett hvordan man kan lage en krets som legger sammen to binære tall. Tilsvarende kan man lage kretser som gjør alle andre operasjoner man trenger i en CPU, som å sammenligne, subtrahere, multiplisere, dividere og så videre. For x86 arkitekturen finnes det hundrevis av instruksjoner, noen krever kompliserte kretser andre er enklere. Ikke alle instruksjoner opererer på tall og data, noen gjør ikke annet enn å endre på verdien av ett enkelt bit. Og kretsene kan utnytte hverandre. Som et eksempel kan man klare å lage en instruksjon som subtraherer ved å kode negative tall med en metode som kalles toerkomplement, kan man bruke en addisjons-krets til å trekke fra hverandre tall også. Kretser for alle de logiske og matematiske instruksjonene legges inn i det som kalles ALU (Arithmetic Logic Unit) og ved å sende riktig styringsbit til ALU, får man utført den instruksjonen man ønsker.