Innholdsoversikt for programutvikling
Appleter er programmer som er beregnet på å skulle kjøres i nettlesere som del av en nettside. Programtypen ble utviklet for å kunne gjøre nettsider interaktive, og ikke bare kunne vise statisk innhold. Den raske populariteten som java i starten fikk som programmeringsspråk, skyldtes i stor grad nettopp muligheten til å lage appleter. Java utviklet seg imidlertid raskt til å bli et generelt programmeringsspråk, slik at muligheten til å lage appleter nå bare er blitt en liten detalj. Selve ordet applet betyr "en liten applikasjon".
Programmeringsmessig er det svært liten forskjell på appleter og applikasjoner. Det går an å
lage programmer som kan kjøres både som applet og som applikasjon. En applet har ingen
main-metode. Isteden må den oppfylle andre formelle krav, blant annet må
den være knyttet til en html-fil.
Siden hensikten med en applet er at den skal være en del av en nettside, og dermed
bli vist i en nettleser, definerer den ikke noe eget vindu på skjermen. Isteden definerer den
en flate innenfor nettleservinduet.
Javas klassebibliotek inneholder to klasser som inneholder det nødvendige rammeverket for en
applet. En applet må defineres i form av en subklasse til en av disse klassene. Den opprinnelige
appletklassen heter nettopp
Applet
og ligger i pakken java.applet.
Men i denne kan vi ikke bruke Javas swing-komponenter. Appleter blir derfor nå til dags
vanligvis definert i form av en subklasse til klassen
JApplet
som må importeres fra pakken
javax.swing. JApplet er i sin tur subklasse til Applet.
I appletklassen vår kan vi legge inn grafiske skjermkomponenter og definere lytteobjekter på
nesten nøyaktig samme måte som vi gjør for vindusklasser. Men det er en viktig forskjell.
For en vindusklasse definerer vi vanligvis en konstruktør der vi legger inn kode for å sette opp
brukergrensesnitt. I main-metoden oppretter vi vindusobjekt og får dermed konstruktørens
instruksjoner utført. For en applet er det nettleseren som oppretter appletobjektet ved hjelp av
appletklassens default-konstruktør, altså den som er uten parametre. Deretter gjør den kall på
appletklassens metode init. På grunn av denne virkemåten, er det for en appletklasse
ikke vanlig å definere noen konstruktør — vi nøyer oss med den systemdefinerte
default-konstruktøren. Isteden redefinerer vi init-metoden og plasserer der den
koden som vi for vindusklasser normalt plasserer i konstruktøren.
For en applet er det noen bestemte metoder som automatisk blir kalt opp når appleten blir aktivert. Noen av dem er det aktuelt å redefinere når vi definerer vår appletklasse. Det gjelder følgende metoder:
public void init()Metoden blir automatisk kalt opp én gang rett etter at appleten er opprettet (av nettleseren). Det er så og si alltid aktuelt å redefinere metoden og legge inn i den kode for initialisering, det vil si kode som vi ellers som regel plasserer i konstruktøren.
public void start()Metoden blir automatisk kalt opp rett etter at init-metoden
er avsluttet. Den blir også automatisk kalt opp dersom brukeren vender tilbake til nettsida som
inneholder appleten, etter at brukeren har surfet innom én eller flere andre nettsider.
Det er derfor aktuelt å redefinere metoden dersom det er kode som vi ønsker utført på nytt
i slike tilfeller. Det kan for eksempel være å starte opp igjen en animasjon.
public void paint(Graphics g)Metoden blir automatisk kalt opp når appleten
blir aktivert, etter at init og start er utført. Den blir også automatisk
kalt opp hver gang det er behov for å tegne opp igjen appletflata på nytt på skjermen, for
eksempel etter at den har vært helt eller delvis dekket av et annet vindu og så blir avdekket igjen. Metoden
utfører ved hjelp av appletens grafikk-kontekst, som er parameter, typiske tegneoperasjoner
på appletflata. Vi skriver aldri selv kode for å gjøre direkte kall på metoden. Dersom vi
av en eller annen grunn ønsker metoden utført, gjør vi isteden kall på metoden
repaint(). Den vil i sin tur gjøre kall på paint.
public void stop()Metoden blir automatisk kalt opp når brukeren forlater den nettsida som inneholder appleten. Det er derfor aktuelt å redefinere den dersom det er bestemte aktiviteter som da skal opphøre, for eksempel kjøring av en animasjon.
public void destroy()Metoden blir kalt opp automatisk når nettleser-sesjonen blir
avsluttet ved at nettleservinduet blir lukket. Metoden har som hensikt å frigjøre ressurser som
er blitt bundet opp av appleten. Som regel er det ikke nødvendig å redefinere metoden. Metoden
stop blir alltid automatisk kalt opp før destroy blir utført.
Appleter er altså ment å være del av en nettside. Under utviklingsarbeidet med en applet, kan det likevel være ønskelig å kunne teste den ut for seg selv, uten at den inngår i noen nettside. Java inneholder derfor et program Applet Viewer som kan vise appleter i et eget vindu på skjermen, slik at vi kan teste dem ut. Dersom vi i Eclipse eller NetBeans skriver en appletklasse som forklart ovenfor og tar vanlig kjørekommando på den, vil den automatisk bli vist i Applet Viewer uten at vi har skrevet noen html-fil for den.
Følgende klasse definerer en applet som viser en liten label-tekst.
Den forutsetter bruk av den såkalte contentPane-delegasjon som er definert
fra og med java-versjon 1.5: add-metoden er programmert til å
tilføye til appletens contentPane den komponent som er parameter.
Default-layout for appletens contentPane er BorderLayout.
Slik koden er skrevet nedenfor, vil det være i CENTER-posisjon at
komponenten blir lagt inn.
1 import javax.swing.JApplet; 2 import javax.swing.JLabel; 3 4 public class Testapplet extends JApplet 5 { 6 public void init() 7 { 8 add( new JLabel("Testapplet", JLabel.CENTER)); 9 } 10 }
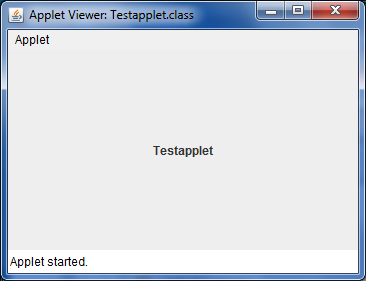
Når vi kjører denne klassen i NetBeans, får vi opp det vindu som er vist på følgende bilde.

Det er også mulig å kjøre Applet Viewer direkte fra
konsollvinduets kommandolinje. Da må vi på kommandolinja skrive appletviewer etterfulgt av et mellomrom
og fullt filnavn for en html-fil med en <applet>-tag for vedkommende
applet. Vi skal se på hvordan en slik html-fil kan se ut.
applet>-tagFølgende html-fil inneholder det som skal til for å kjøre appleten definert ovenfor.
<html>
<head>
<title>Testapplet</title>
</head>
<body>
<applet code="Testapplet.class" width="300" height="100">
</applet>
</body>
</html>
Legg merke til at vi i <applet>-taggen spesifiserer hvilken fil som definerer appleten, samt setter bredde og høyde på den i antall piksler. Slik angivelsen av class-fil er skrevet, forutsettes det at fila ligger i samme filkatalog som html-fila. Setter vi ikke høyde og bredde riktig, vil appleten ikke bli vist. Som for vinduer, må vi ofte prøve oss litt fram for å finne en passe størrelse for appleten.
Når html-fil for appleten er skrevet og dens class-fil er riktig angitt og plassert, kan vi få kjørt appleten ved å vise vedkommende html-fil i en nettleser. Nettleseren må være oppsatt til å tillate visning av appleter. Det er ikke alle som er det. Følgende bilde viser resultatet av å vise appleten ovenfor i en nettleser.
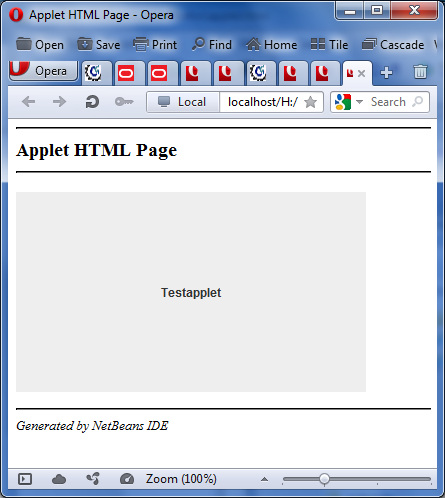
Dersom din egen nettleser er satt opp for å vise appleter, kan du få kjørt appleten ovenfor ved å klikke på følgende link: testapplet.html.
En applet bør for øvrig testes ut i flere forskjellige nettlesere og versjoner av disse før vi legger den ut på nettet. Vi har ingen garantier for at nettleserne vil vise appleten vår på samme måte.
I eksemplet ovenfor er det i <applet>-taggen bare tatt med de attributtene som er obligatoriske for å få kjørt appleten i en nettleser. Det finnes i tillegg noen attributter som det er frivillig å ta med, men som noen ganger kan være nyttige. Det er følgende attributter:
codebase = applet_url archive = arkivfil vspace = vertikalmarg hspace = horisontalmarg align = vindusplassering alt = tekstalternativ
De frivillige attributtene har følgende betydning:
codebase spesifiserer hvor appletens
class-fil(er) skal hentes fra.
Dersom det er en annen katalog enn den som html-fila ligger i, må vi angi
plasseringen i form av en nettadresse.archive instruerer nettleseren til å laste inn en arkivfil (jar-fil) som
inneholder alle filene som er nødvendige for å kjøre appleten. Når appleten
trenger flere filer, kan vi ved å pakke dem i en arkivfil få redusert nedlastingstiden
og forbedret effektiviteten.vspace og hspace spesifiserer størrelse, i antall piksler,
for det tomme rommet som vi ønsker å legge på hver side av appletflata, vertikalt og
horisontalt.align spesifiserer hvordan appletflata skal plasseres i nettleser-vinduet.
En av følgende ni verdier kan tilordnes: left, right, top, texttop, middle,
absmiddle, baseline, bottom, eller absbottom.alt spesifiserer hvilken tekst som skal vises istedenfor appleten,
dersom nettleseren ikke kan kjøre den.Som du ser av html-fila for eksemplet Testapplet ovenfor, setter vi
i html-fila størrelse for appleten i antall piksler. Dette er nødvendig for å få den
vist i en nettleser. Men
som nevnt ovenfor, kan vi i Eclipse og NetBeans kjøre appleter uten at det er definert noen
html-fil for appleten. De vil da selv sette en standardstørrelse for det vinduet som
visningsprogrammet Applet Viewer viser. I eksemplet ovenfor kan du se hvor
stort dette er i NetBeans. Det er klart at denne standardstørrelsen sjelden vil passe. For uttesting
av appleter ved å kjøre dem i Eclipse eller NetBeans er det derfor ønskelig å få satt størrelse på annen måte.
Det får vi gjort ved å bruke setSize-metoden i appletens
init-metode på tilsvarende måte som i følgende eksempel.
1 import javax.swing.JApplet; 2 import javax.swing.JLabel; 3 import java.awt.Dimension; 4 5 public class Testapplet extends JApplet 6 { 7 public void init() 8 { 9 setSize( new Dimension( 400, 100 )); 10 add( new JLabel("Testapplet", JLabel.CENTER)); 11 } 12 }
Følgende bilde viser resultatet av å kjøre denne appleten i NetBeans ved bruk av Applet Viewer.
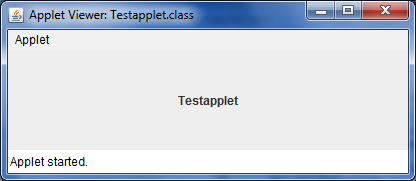
Når en applet blir kjørt i nettleser, vil
den størrelsen som blir satt i init-metoden bli overstyrt av den størrelsen som
settes i html-fila.
De enkle eksemplene ovenfor har ikke vært interaktive, slik at de har kunnet gjøre nettsider dynamiske. Vi skal nå ta for oss et eksempel på animasjon, der brukeren kan påvirke animasjonen.
Vi skal lage en applet som simulerer pendelbevegelse. Vi tenker oss at pendelen består av en kule opphengt fritt i en snor, slik at kula kan svinge fram og tilbake. Vi kaller pendelens utslagsvinkel, målt i radianer, for θ. (Utslagsvinkelen er vinkelen mellom pendelsnora og en loddlinje gjennom pendelsnoras opphengspunkt.) Når pendelen svinger, vil da utslagsvinelen være bestemt av formelen
θ = θo e-kt cos (ωt)
Her er
| θo: | maksimal utslagsvinkel |
| k: | dempningsfaktor (på grunn av luftmotstand etc.) |
| ω: | vinkelhastighet |
| t: | tid |
Dersom k = 0, får vi θ = θo cos (ωt).
Programmet skal tegne bilder av pendelen, et nytt bilde med pendelen i en ny posisjon hver gang animasjonsløkka blir gjennomløpt. Bildet av pendelen består av en rett linje og en fylt sirkel. Linja har ett fast endepunkt: svarende til opphengspunktet for pendelsnora. Vi må finne posisjonen for det andre endepunktet. For sirkelen må vi finne basisposisjonen som den skal tegnes fra, ny posisjon for hver gang. (Basisposisjonen er posisjonen for det øverste venstre hjørne i det omskrevne rektanglet.) Vi setter navn på de nødvendige koordinater og størrelser:
| (xo, yo): | koordinatene for pendelsnoras faste endepunkt |
| L: | pendelsnoras lengde |
| (x, y): | koordinatene for pendelsnoras bevegelige endepunkt |
Da vil følgende formler gjelde:
x = xo + L sin θ
y = yo + L cos θ
Dersom vi kaller koordinatene til basisposisjonen for sirkelen ("pendelkula") for (xb, yb) og radien til sirkelen for R, så vil følgende formler gjelde:
xb = x - R(1 - sin θ)
yb = y - R(1 - cos θ)
Disse formlene må vi bruke for beregning av ny posisjon for pendelen. For å simulere tid bruker vi en heltallsvariabel som vi kan tenke på som sekund. Den øker vi med én hver gang animasjonsløkka blir gjennomløpt.
Klassen Pendel som er gjengitt nedenfor representerer en slik pendel.
Lengden til pendelsnora og posisjonen for dens opphengspunkt mottas som konstruktørparametre.
Dempningsfaktoren settes i utgangspunktet lik 0, men den kan endres ved hjelp av en
set-metode. Metoden tegnPendel tegner pendelen i en gitt
posisjon ved bruk av formlene som er omtalt ovenfor. Pendelens nye posisjon for tidspunktet
t blir beregnet av metoden flytt. Dersom pendelen ikke har noen dempning,
vil den svinge så lenge som appleten kjører. Dersom det er lagt inn dempning, vil de maksimale utslagene bli
mindre og mindre. Det er da fornuftig å stoppe animasjonsløkka når det maksimale utslaget blir mindre enn en
viss grense. Til dette formål brukes metoden svingende. Metoden
nullstill har til hensikt å kunne gjøre det mulig å starte opp igjen animasjonen "på ny frisk" ved at
den setter maksimal utslagsvinkel til 30 grader.
1 import java.awt.Graphics; 2 import javax.swing.JPanel; 3 4 public class Pendel extends JPanel 5 { 6 private int x0, y0; //posisjon for pendelsnoras øverste ende 7 private int x, y; //posisjon for pendelsnoras nederste ende 8 private final int DIAM = 20; //pendelkulas diameter 9 private double k; //dempningsfaktor 10 private double theta0 = Math.PI / 6; //startvinkel lik 30 grader 11 private double theta; //utslagsvinkel 12 private double omega = 7.0; //vinkelhastighet 13 private double grense = 0.005; //nedre grense for maksimalt utslag 14 private int snorlengde; //pendelsnoras lengde 15 16 public Pendel(int xpos, int ypos, int lengde) 17 { 18 x0 = xpos; 19 y0 = ypos; 20 snorlengde = lengde; 21 k = 0; //kjører uten dempning om ikke annet er valgt 22 } 23 24 public void setDempning(double dempningsfaktor) 25 { 26 k = dempningsfaktor; 27 } 28 29 public void paintComponent(Graphics g) 30 { 31 super.paintComponent(g); 32 tegnPendel(g); 33 } 34 35 public void tegnPendel(Graphics g) 36 { 37 double s = Math.sin(theta); 38 double c = Math.cos(theta); 39 //finner basispunkt for tegning av pendelkule: 40 int xb = x - (int) (DIAM * (1 - s) / 2); 41 int yb = y - (int) (DIAM * (1 - c) / 2); 42 g.fillOval(xb, yb, DIAM, DIAM); 43 g.drawLine(x0, y0, x, y); 44 } 45 46 //regner ut ny posisjon for pendelkula 47 public void flytt(long t) 48 { 49 theta0 *= Math.exp(-k * t / 100); 50 theta = theta0 * Math.cos(omega * t / 100); 51 x = x0 + (int) (snorlengde * Math.sin(theta)); 52 y = y0 + (int) (snorlengde * Math.cos(theta)); 53 } 54 55 public boolean svingende() 56 { 57 return (theta0 > grense); 58 } 59 60 public void nullstill() 61 { 62 theta0 = Math.PI / 6; 63 } 64 }
Selve appletklassen er gjengitt nedenfor. Datafeltet bps bestemmer
hvor mange ganger per sekund pendelen skal tegnes på nytt i en ny posisjon, eller
med andre ord: hvor mange nye bilder av pendelen per sekund.
Drivverket for animasjonen er
Timer-objektet klokke. Den er satt opp til å generere
en ActionEvent så mange ganger hvert sekund som er bestemt av datafeltet
bps. Appleten fungerer som lytteobjekt for
Timeren, slik at appletens actionPerformed-metode blir kalt opp
så mange ganger hvert sekund som er bestemt av datafeltet for antall bilder per sekund.
Dersom pendelen er i bevegelse, øker actionPerformed-metoden
tiden med én (simulering av
at det har gått en bps-del av et sekund), flytter pendelposisjonen og tegner pendelen i ny posisjon.
(En nærmere beskrivelse av Timer-klassen kan du finne i notatet
Hva er en Timer?.)
Appletens start- og stop-metoder er programmert til å starte og
stoppe animasjonen, ved at de gjør kall på metodene startAnimasjon og
stoppAnimasjon. Disse metodene starter og stopper animasjonen ved kall på
Timerens start- og stop-metoder.
Som tidligere nevnt, er pendelens dempningsfaktor i utgangspunktet satt til null. Brukeren har anledning til å skrive inn ønsket verdi for dempningsfaktoren i appletens tekstfelt. Når verdi leses inn og registreres, blir animasjonen nullstilt og startet opp igjen på nytt.
For pendelpanelet er det registrert en muselytter, definert av den indre klassen
Muselytter. Denne gjør det mulig for brukeren å stoppe og starte animasjonen
ved å klikke med en museknapp.
De to klassene som definerer appleten kan du laste ned ved å klikke på linkene
Pendel.java og
Pendelbevegelse.java.
1 import java.awt.*; 2 import java.awt.event.*; 3 import javax.swing.*; 4 5 public class Pendelbevegelse extends JApplet implements ActionListener 6 { 7 private JTextField input, output; 8 private Pendel pendel; 9 private Timer klokke; 10 private long tid; 11 private boolean fastFryst = false; 12 private int bps = 20; //antall bilder pr. sekund 13 private int pauselengde = 1000 / bps; //tid mellom hvert nytt bilde 14 private int y0 = 20; //avstand fra øvre kant til pendelsnoras 15 //festepunkt 16 17 public void init() 18 { 19 setSize(new Dimension(700, 500)); 20 JPanel np = new JPanel(); 21 np.add(new JLabel("Velg dempingsfaktor:")); 22 input = new JTextField(4); 23 input.addActionListener(this); 24 np.add(input); 25 output = new JTextField(20); 26 output.setEditable(false); 27 np.add(output); 28 klokke = new Timer(pauselengde, this); 29 klokke.setInitialDelay(0); 30 klokke.setCoalesce(true); 31 tid = 0L; 32 Container c = getContentPane(); 33 c.add(np, BorderLayout.PAGE_START); 34 Dimension dim = getSize(); 35 if (dim.height - 100 > 50) 36 { 37 pendel = new Pendel(dim.width / 2, y0, dim.height - 100); 38 pendel.addMouseListener(new Muselytter()); 39 c.add(pendel, BorderLayout.CENTER); 40 } 41 else 42 { 43 output.setText("For lav applet."); 44 } 45 } 46 47 public void start() 48 { 49 startAnimasjon(); 50 } 51 52 public void stop() 53 { 54 stoppAnimasjon(); 55 } 56 57 public synchronized void startAnimasjon() 58 { 59 if (!fastFryst) 60 { //starter animasjon 61 if (!klokke.isRunning()) 62 { 63 klokke.start(); 64 } 65 } 66 } 67 68 public synchronized void stoppAnimasjon() 69 { 70 if (klokke.isRunning()) //stopper animasjonstråden 71 { 72 klokke.stop(); 73 } 74 } 75 76 public void actionPerformed(ActionEvent e) 77 { 78 if (e.getSource() == input) 79 { 80 try 81 { 82 double dempningsfaktor = Double.parseDouble(input.getText()); 83 pendel.setDempning(dempningsfaktor); 84 stoppAnimasjon(); 85 pendel.nullstill(); 86 tid = 0L; 87 pendel.flytt(tid); 88 klokke.setInitialDelay(0); 89 startAnimasjon(); 90 } 91 catch (NumberFormatException ex) 92 { 93 output.setText("Galt tallformat. Prøv igjen!"); 94 } 95 } 96 else if (pendel.svingende()) 97 { 98 pendel.flytt(tid++); 99 pendel.repaint(); 100 } 101 } 102 103 private class Muselytter extends MouseAdapter 104 { 105 public void mousePressed(MouseEvent e) 106 { 107 if (fastFryst) 108 { 109 fastFryst = false; 110 startAnimasjon(); 111 } 112 else 113 { 114 fastFryst = true; 115 stoppAnimasjon(); 116 } 117 } 118 } 119 }
Ved at du klikker på følgende link, skal du få kjørt apppleten i din nettleser: Kjør animasjon!.
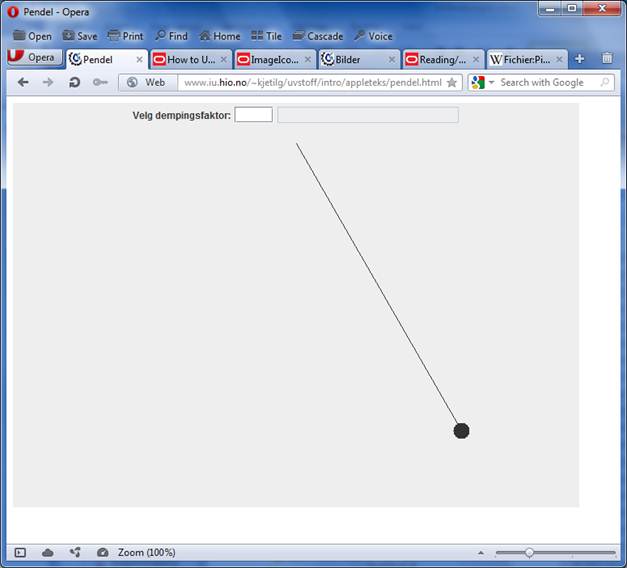
Følgende bilde gir et øyeblikksbilde av den svingende pendelen.
Vi skal lage en applet som suksessivt kan tegne de kurvene som danner grunnlaget for den såkalte fraktalkurva som kalles Kochs snøflakkurve. Kurva framkommer ved å ta utgangspunkt i en likesidet trekant som vist på følgende bilde.
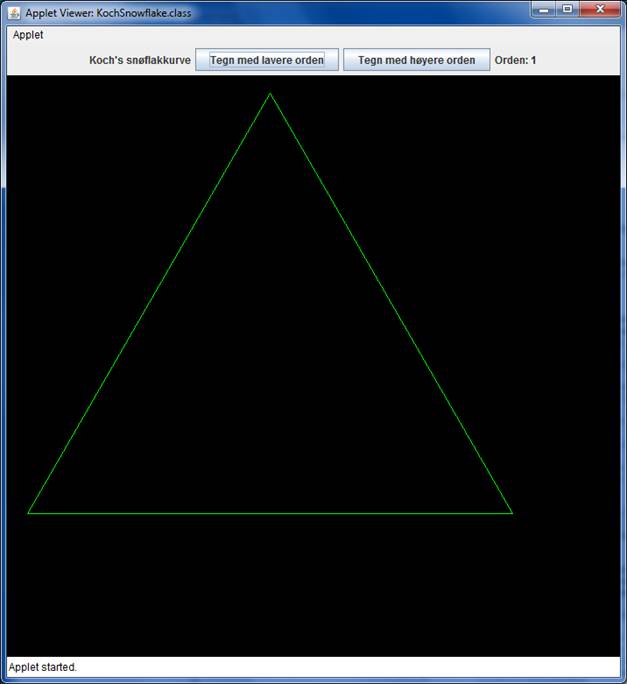
Denne trekanten skal vi kalle kurve av orden 1. For å utvikle den rekursive
metoden som kan tegne kurver av høyere ordener, skal vi nå ta for oss én av
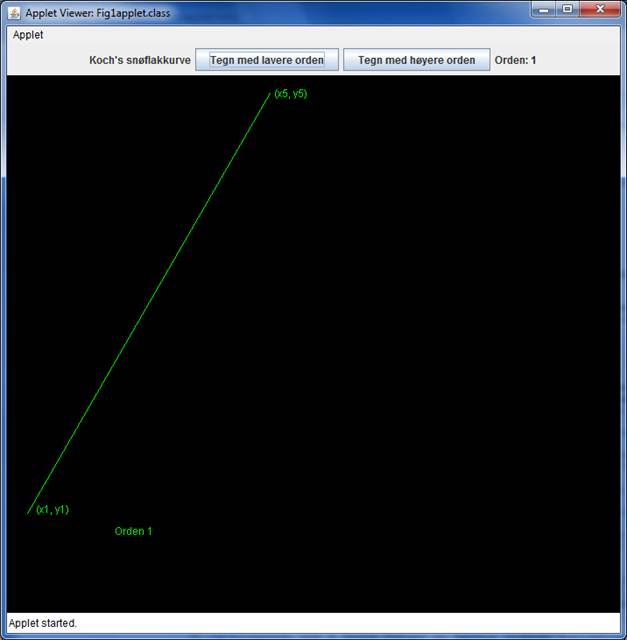
sidene i denne trekanten og sette navn (x1, y1), (x5, y5)
på koordinatene til endepunktene, slik det er vist på neste bilde.
For å få kurve av orden 2, blir hver av de rette linjene på kurve av orden 1 erstattet med en brukket linje tilsvarende som vist på følgende figur for den ene linja på foregående figur.
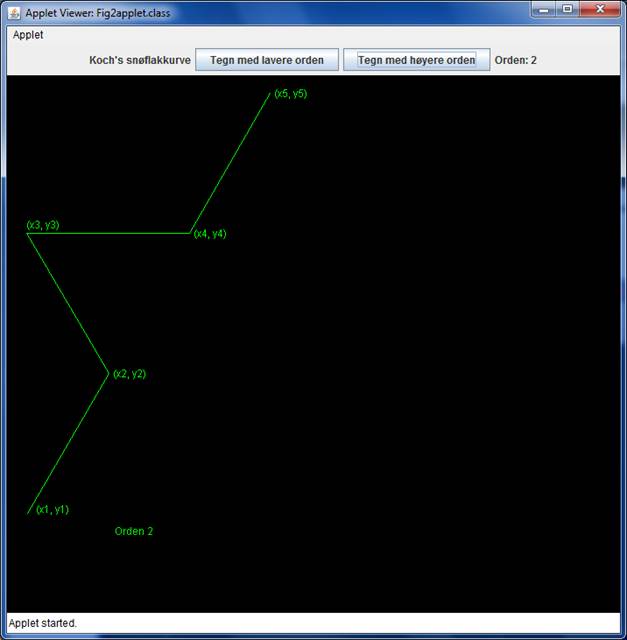
På figuren har vi navngitt de nye hjørnene med (x2, y2), (x3, y3) og
(x4, y4). Hver bit av den nye, brukne linja har en lengde lik 1/3 (en tredel)
av den opprinnelige, rette linja fra kurve av orden 1.
Prosessen med å danne kurver av høyere ordener fortsetter på samme måte: Hver rett linje erstattes av en brukket linje tilsvarende som ved overgangen fra orden 1 til orden 2. Neste skritt på den kurve som er vist på siste figur, vil gi følgende figur.

Det som går under navn av Kochs snøflakkurve, får vi ved å fortsette den nevnte prosessen i det uendelige. Det vi skal gjøre, er å lage en applet som suksessivt kan vise kurver av høyere og høyere ordener, inntil noen av enkeltbitene blir så små at det ikke har noen hensikt å fortsette videre på grunn av begrenset skjermoppløsning.
For å komme fram til den rekursive metoden for å tegne kurvene av forskjellige ordener, gjør vi nå følgende observasjoner:
Koordinatene for punktene med indeksverdier 2, 3 og 4 bestemmer vi på grunnlag av
koordinatene for punktene med indeksverdier 1 og 5 slik at avstanden mellom to punkter som
følger etter hverandre er en tredel av avstanden mellom (x1, y1) og
(x5, y5). Bruk av enkel matematikk gir formlene
x2 = x1 + (x5 - x1)/3 y2 = y1 + (y5 - y1)/3 x3 = (x1 + x5)/2 + 3½(y1 - y5)/6 y3 = (y1 + y5)/2 + 3½(x5 - x1)/6 x4 = x1 + 2(x1 + x5)/3 y4 = y1 + 2(y1 + y5)/3
Det er klart at koordinatene x1, y1, x5, y5, samt kurvas orden,
må være parametre i den rekursive metoden som skal tegne kurve av en gitt orden.
Det metoden må gjøre, er å beregne koordinatene til de tre nye punktene ved å bruke
formlene ovenfor. Og så må metoden tegne en kurve av orden én lavere mellom to
og to punkter som følger etter hverandre. Dessuten må den, selvsagt, sjekke om det
dreier seg om et basistilfelle. I følgende metode, som implementerer denne virkemåten,
er det brukt konstanten
8 private double SQ = Math.sqrt(3.0) / 6; //brukes i koordinatberegning
som inngår i to av formlene ovenfor.
21 public void tegnFraktal(int orden, int x1, int y1, int x5, int y5, 22 Graphics g) 23 { 24 if (orden == 1) 25 { 26 g.drawLine(x1, y1, x5, y5); 27 } 28 else 29 { 30 int deltaX = x5 - x1; 31 int deltaY = y5 - y1; 32 int x2 = x1 + deltaX / 3; 33 int y2 = y1 + deltaY / 3; 34 int x3 = (int) ((x1 + x5) / 2 + SQ * (y1 - y5)); 35 int y3 = (int) ((y1 + y5) / 2 + SQ * (x5 - x1)); 36 int x4 = x1 + deltaX * 2 / 3; 37 int y4 = y1 + deltaY * 2 / 3; 38 39 tegnFraktal(orden - 1, x1, y1, x2, y2, g); 40 tegnFraktal(orden - 1, x2, y2, x3, y3, g); 41 tegnFraktal(orden - 1, x3, y3, x4, y4, g); 42 tegnFraktal(orden - 1, x4, y4, x5, y5, g); 43 } 44 }
I programmet som skal gjøre bruk av den rekursive tegnemetoden, må vi bestemme
hvilken trekant som skal være kurve av orden 1, det vil si vi må bestemme hjørnenes
koordinater. Det må gjøres kall på den rekursive tegnemetoden for hver av de tre
sidene i basistrekanten. Klassen KochPanel som er gjengitt nedenfor
definerer et tegnepanel for kurva. Klassen inneholder konstanter for koordinatene
i basistrekantens hjørner. Panelets paintComponent-metode foretar kall
på den rekursive tegnemetoden for hver av basistrekantens sider, og med den orden som
er satt. For ordenen er det set- og get-metoder.
Java-fil for klassen kan lastes ned ved å klikke på linken
KochPanel.java
1 import java.awt.*; 2 import javax.swing.*; 3 4 public class KochPanel extends JPanel 5 { 6 private final int BREDDE = 600; 7 private final int HØYDE = 600; 8 private double SQ = Math.sqrt(3.0) / 6; //brukes i koordinatberegning 9 private final int TOPPX = 300, TOPPY = 20;//koordinater for hjørner i 10 private final int VENSTREX = 23, VENSTREY = 500; //likesidet trekant, 11 private final int HØYREX = 577, HØYREY = 500; //dvs. kurve av orden 1 12 private int ønsketOrden; //orden for kurve som skal tegnes (1,2, ...) 13 14 public KochPanel(int startorden) 15 { 16 ønsketOrden = startorden; 17 setBackground(Color.black); 18 setPreferredSize(new Dimension(BREDDE, HØYDE)); 19 } 20 21 public void tegnFraktal(int orden, int x1, int y1, int x5, int y5, 22 Graphics g) 23 { < som ovenfor > 44 } 45 46 public void paintComponent(Graphics g) 47 { 48 super.paintComponent(g); 49 g.setColor(Color.green); 50 tegnFraktal(ønsketOrden, TOPPX, TOPPY, VENSTREX, VENSTREY, g); 51 tegnFraktal(ønsketOrden, VENSTREX, VENSTREY, HØYREX, HØYREY, g); 52 tegnFraktal(ønsketOrden, HØYREX, HØYREY, TOPPX, TOPPY, g); 53 } 54 55 public void setOrden(int orden) 56 { 57 ønsketOrden = orden; 58 } 59 60 public int getOrden() 61 { 62 return ønsketOrden; 63 } 64 }
Appletklasse som bruker tegnepanelet er gjengitt nedenfor. Du kan laste den ned fra linken
KochSnowflake.java.
Klassen inneholder funksjonalitet for brukeren til å velge med hvilken orden
kurva skal tegnes. På grunn av begrenset oppløsning på skjermen, er det ingen
vits i å tegne kurver av høyere orden enn 9. Du kan kjøre appleten ved å klikke
på linken KochApplet.
1 import java.awt.*; 2 import java.awt.event.*; 3 import javax.swing.*; 4 5 public class KochSnowflake extends JApplet implements ActionListener 6 { 7 private final int APPLETBREDDE = 700, APPLETHØYDE = 700; 8 private final int MIN = 1, MAX = 9; 9 private JButton øk, mink; 10 private JLabel orden; 11 private KochPanel tegning; 12 13 public void init() 14 { 15 øk = new JButton("Tegn med høyere orden"); 16 mink = new JButton("Tegn med lavere orden"); 17 øk.addActionListener(this); 18 mink.addActionListener(this); 19 JPanel nordp = new JPanel(); 20 nordp.add(new JLabel("Koch's snøflakkurve")); 21 nordp.add(mink); 22 nordp.add(øk); 23 orden = new JLabel("Orden: 1"); 24 nordp.add(orden); 25 tegning = new KochPanel(MIN); 26 Container c = getContentPane(); 27 c.add(nordp, "North"); 28 c.add(tegning, "Center"); 29 setSize(APPLETBREDDE, APPLETHØYDE); 30 } 31 32 public void actionPerformed(ActionEvent e) 33 { 34 int kurveorden = tegning.getOrden(); 35 if (e.getSource() == øk) 36 { 37 kurveorden++; 38 } 39 else 40 { 41 kurveorden--; 42 } 43 44 if (kurveorden >= MIN && kurveorden <= MAX) 45 { 46 orden.setText("Orden: " + kurveorden); 47 tegning.setOrden(kurveorden); 48 repaint(); 49 } 50 } 51 }
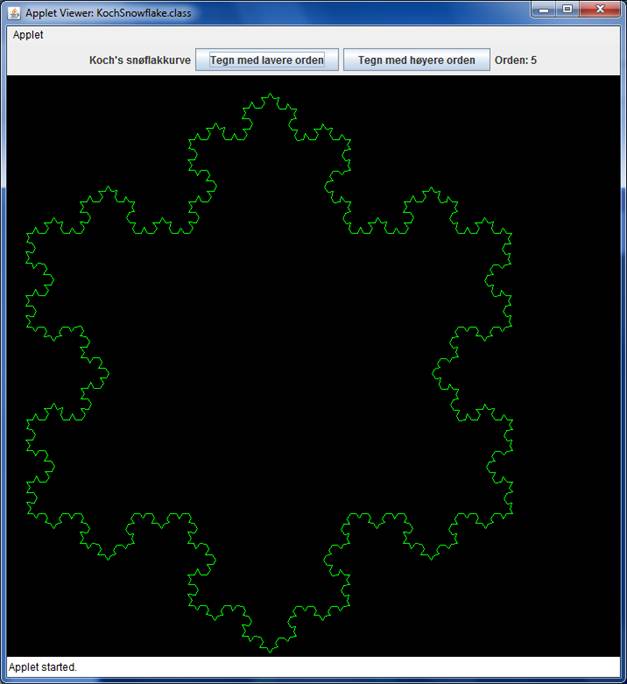
Følgende bilde viser en kurve av orden 5.
Innholdsoversikt for programutvikling
Copyright © Kjetil Grønning og Eva Hadler Vihovde, revidert 2012